这个模型是在微信公众号上看到的，原文叫3578模型，因为每个三角形都含有7这个边，所以这里稍微改了一下，把7放在了最后。

在实际解题中没有太大用处，倒是有可能出现在材料阅读题中，所以可以当成一个比较有趣的材料阅读来探究。

一、特殊三角形

初中阶段，我们学习了不少特殊三角形，比如三角板三角形（含30°角的直角三角形、等腰直角三角形）、黄金三角形（有一个角是36°的等腰三角形）、有一个角是30°的等腰三角形（底角30°的比较常见）。

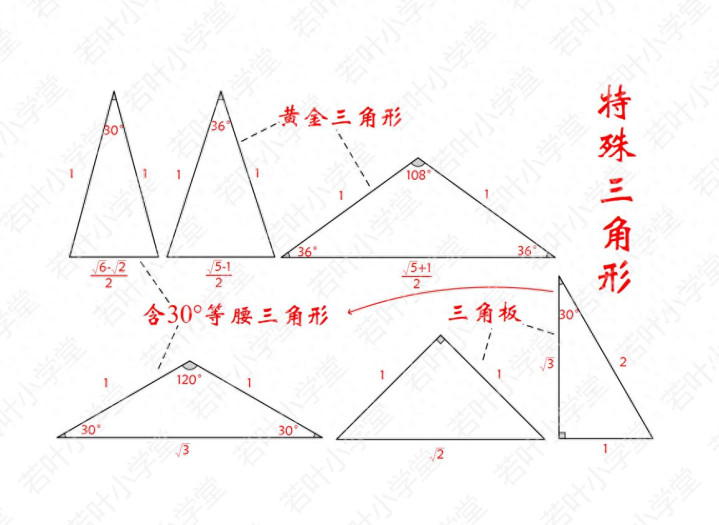
那有没有这样一种三角形：三边长都是整数，且含有特殊角的三角形？

二、3587模型

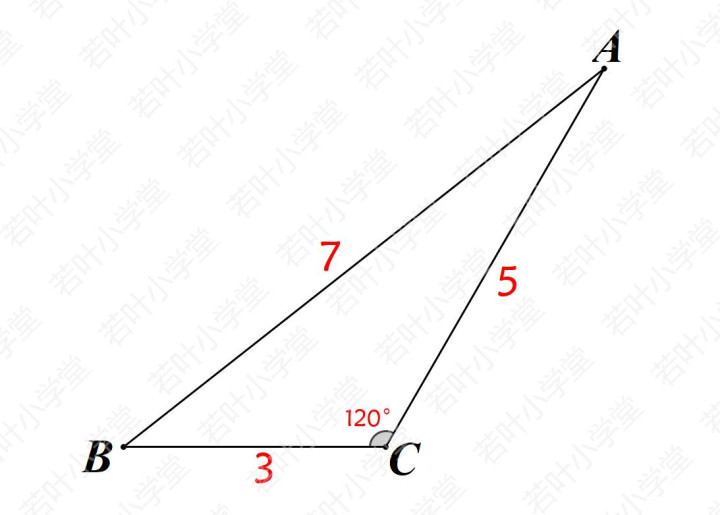
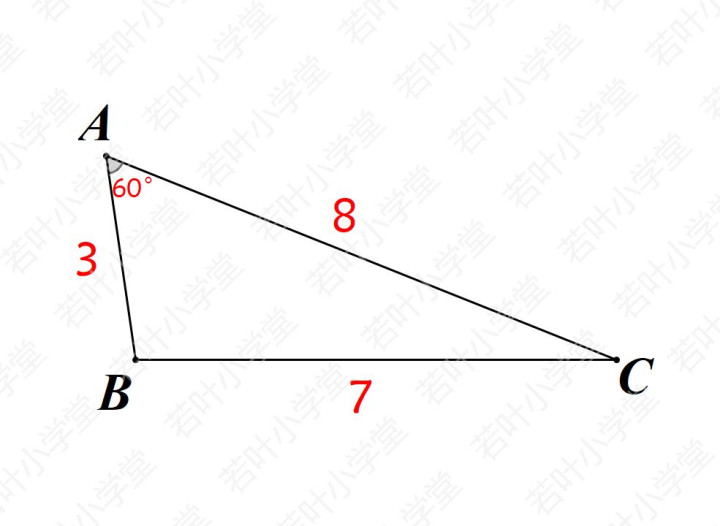
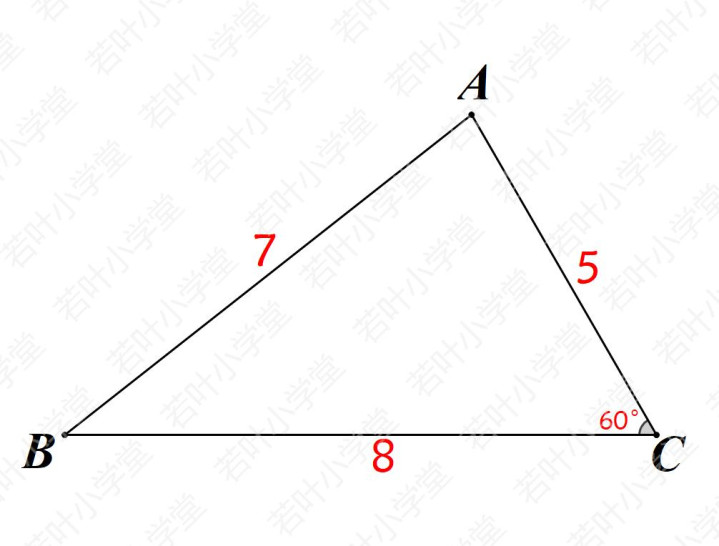
3587模型是指边长分别为357、387、587的3个特殊三角形，其中357含120°角，387和587含60°角。

1、357三角形

2、387三角形

3、587三角形

这三个三角形还能拼成一个等边三角形。

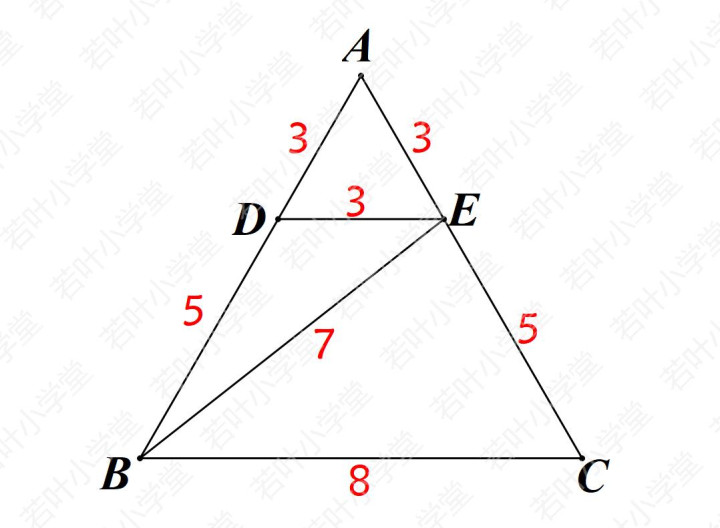
那还有没有类似的三角形呢？相似三角形除外，也就是边长不能是3587模型三角形的整数倍。

三、寻找类似三角形

首先要明确目标：有一个角是60°或120°，三边长都是整数且互质的三角形。

解决方案：AI辅助，先让AI跑一遍，然后找找规律。

试了几个AI，跑停的，跑错的，跑漏的层出不穷，最后结合AI分析过程，把边长限制在50范围内，共找到了12个含60°的互质边三角形，6个含120°的互质边三角形，如果组成等边三角形，类似3587模型这样，一共有6组。

根据下面公式自己就可以推导或验证，第一行公式是由余弦定理得到，第二行公式是由第一行公式变形后得到，方便笔算推导或验证。

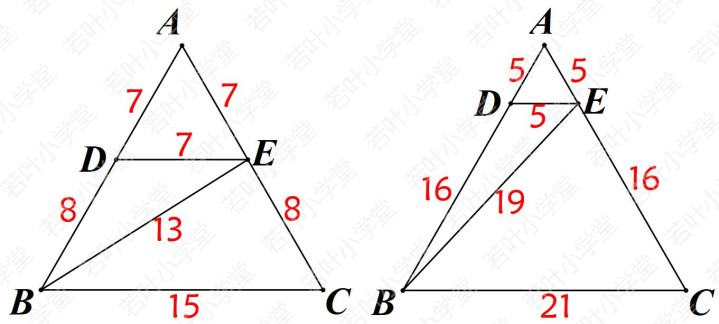
第二组、第三组拼成等边三角形后如下图所示：

最后说一句：目前解数学题没有一个AI是靠得住的，简单题或许还行，稍微上点儿难度就容易出问题，如果实在没思路可以尝试问一下AI，但是要多问几个模型（同一个AI通常会有好几个模型可供选择）、多问几个AI，然后综合一下，不要迷信各种宣传，要实际体验。